Wait But Why tient un séminaire à l’attention de tous ses petits personnages en bâtons. Tout le monde s’en réjouit d’avance — c’est l’occasion d’apprendre à se connaître un peu mieux, ce qui est exceptionnel, car ils sont généralement captifs de leur dessins, et ne peuvent se sociabiliser.
Cependant, les choses tournent rapidement au vinaigre, puisque Wait But Why leur annonce que tout le monde ne sera pas reconduit dans la boîte, suite à une réduction d’effectif.
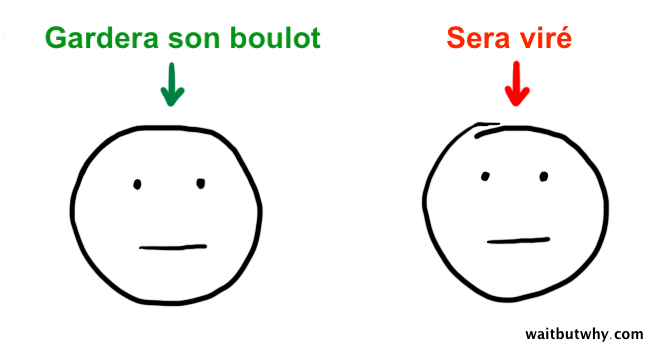
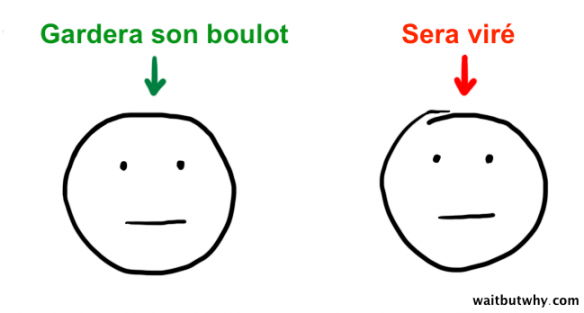
La décision prise est que tous les bonhommes avec une tête parfaitement circulaire garderont leur boulot, et ceux avec une tête que Tim a foiré en ne reliant pas correctement le cercle seront gommés.
Le problème, c’est que les bonhommes ne peuvent pas se regarder dans un miroir, et il n’y absolument aucun moyen pour eux de savoir à quoi leur propre tête pourrait ressembler. Ils peuvent voir la tête de tous les autres personnages, mais pas la leur.
Pour échapper au malaise provoqué par l’annonce de leur plan de licenciement, Tim et Andrew ont préféré énoncer les règles suivantes et se retirer en douce du séminaire :
Règle n°1 : Dorénavant, ne sera faite aucune mention de l’état de la tronche de qui que ce soit, pas même par le biais d’expressions faciales ou de langage corporel susceptibles de renseigner autrui à ce sujet.
Règle n°2 : Si vous veniez à découvrir que votre tête est loupée, vous êtes priés de bien vouloir vous gommer le soir même à minuit.
Règle n°3 : Tous les personnages en bâtons sont tenus d’observer scrupuleusement les règles en toute circonstance, de faire preuve d’une logique infaillible, et être conscients que tous les autres font de même.
Règle n°4 : Il convient de prendre note que sont ici présents au séminaire 100 personnages en bâtons, et au moins un d’entre eux a une tête ratée.
Troublés, le Jour 1 de nos bonhommes en séminaire suit son cours, et ils essaient d’en profiter du mieux possible. Cette nuit-là, à 22h, tout le monde rejoint sa chambre pour aller se coucher.
Le jour suivant (Jour 2), les personnages en bâtons se retrouvent pour démarrer leur journée, et tout le monde est encore là. Même tableau le Jour 3. En fait, c’est exactement la même histoire jusqu’au Jour 8.
Mais lorsque les bonhommes émergent de leur chambre au petit matin du Jour 9, seuls restent ceux qui ont des têtes parfaites. Il semble que tous ceux qui avaient une tête ratée se sont gommés la nuit du Jour 8.
La question est : Combien de bonhommes se sont gommés le soir du Jour 8 et pourquoi les choses se sont déroulées ainsi ?
Ceci est basé sur un célèbre casse-tête de logique. Réfléchissez-y bien avant de regarder la solution. Ci-dessous, deux indices à disposition, pour vous aider en cas de panne sèche.
INDICE 1
INDICE 2
SOLUTION
Huit bonhommes se sont gommés durant le Jour 8. Voici pourquoi :
Commencez par réfléchir au cas de figure présentant seulement un seul bonhomme avec une tête loupée. Jour 1, il jetterait un œil à la pièce, ne verrait personne avec une tête loupée, et comprendrait alors qu’il était nécessairement celui à la tête foirée (puisque la Règle n°4 stipule qu’au moins l’un des personnages en bâtons a une tête loupée). Dans la mesure où il doit s’acquitter de son serment (Règle n°3), il s’auto-gommera cette nuit-là.
Maintenant, imaginez qu’il n’y a pas un, mais deux bonhommes à la tête ratée — appelons-les Mec A et Mec B. Pendant le Jour 1, Mec A et Mec B vont faire un petit tour d’horizon, et constater qu’un bonhomme a une tête imparfaite, là où les 98 autres ont une tête irréprochable. Mec A suppose alors que Mec B ne verra personne avec une tête ratée, qu’il en déduira qu’il doit en avoir une, et que ce dernier se gommera cette nuit-là.
Mais arrivé au Jour 2, Mec A voit Mec B débarquer au petit matin en un seul morceau, et il comprend alors que Mec B a dû aller se coucher sans savoir que sa tête était ratée. La seule explication possible, sachant que Mec B est au jus qu’au moins une personne a la tête ratée, et que Mec B a vu quelqu’un d’autre avec une tête loupée. Comme Mec A a vu des têtes parfaites chez les 98 autres bonhommes, il en conclut qu’il doit nécessairement lui aussi avoir une tête chelou.
Mec B suit le même cheminement de pensée. Au Jour 2, ils savent tous deux qu’ils ont des têtes ratées et s’auto-gomment à minuit.
L’étape suivante, qui recense trois bonhommes avec une tête ratée (Mec A, B et C), révèle qu’au Jour 1, tout le monde voit trois têtes loupées, exceptés ceux qui en ont effectivement une : ces derniers n’en voient que deux. Donc Mec A examine Mec B et Mec C et se dit “Ces deux-là ne réalisent pas qu’ils ont une tête chelou, et peuvent seulement constater que l’autre en a une — donc ils vont s’attendre à ce que l’autre s’auto-gomme à la nuit du Jour 1. Mais au Jour 2, ils vont se revoir et comprendre qu’en réalité, ils ont, eux aussi, une tête chelou — et ils se gommeront donc à la nuit du Jour 2”. Néanmoins, lorsque Mec A se réveille au matin du Jour 3 et aperçoit à la fois Mec B et Mec C sain et sauf, il est frappé par l’idée qu’il doit lui-même avoir une tête ratée — en concordance avec l’hypothèse que Mec B et Mec C se couche à la fin du Jour 2 en ignorant toujours la nature de leur tête.
Mec B et Mec C ont la même révélation au Jour 3, et, cette nuit-là, tous les trois se donnent la gomme.
En répétant ce schéma, si le Jour 8 est celui où les gommages ont finalement lieu, il y avait nécessairement huit bonhommes avec des têtes loupées. Chacun d’entre eux aurait respectivement vu sept autres têtes chelous pendant le séminaire, et tous auraient présumé, en allant se coucher Jour 7, que cette nuit serait celle des gommages. Lorsque toutes les têtes loupées débarquent Jour 8, chacune d’entre elles réalisent soudain qu’elles font aussi parties de l’équipe.
C’est clair ? C’est ce que vous aviez trouvé ?